Egy iskolának 510 tanulója van. Év végén a fiúk p százaléka, a lányok p + 3 százaléka lett kitűnő, így 13 fiú és 20 lány kitűnő tanuló van.
a) Határozza meg a fiúk és a lányok számát ebben az iskolában!
A 33 kitűnő (5,0 átlagú) tanuló közül sorsolással kiválasztanak hármat, akik ingyenes nyári táborozást nyernek.
b) Határozza meg annak a valószínűségét, hogy a kisorsolt tanulók között 1 fiú és 2 lány lesz!
Az 510 tanuló év végi tanulmányi átlagairól (a kitűnők számán kívül) még a következő információkat tudjuk: az év végi átlagok terjedelme 2,4; módusza 3,8; mediánja 4,0; átlaga 4,2; szórása 0,9; alsó kvartilise 3,3; felső kvartilise 4,6.
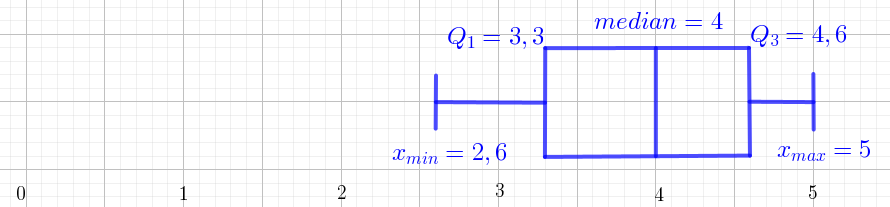
c) Készítsen a tanulók év végi tanulmányi átlagairól sodrófadiagramot!

Egy iskolának 510 tanulója van. Év végén a fiúk p százaléka, a lányok p + 3 százaléka lett kitűnő, így 13 fiú és 20 lány kitűnő tanuló van.
a) Határozza meg a fiúk és a lányok számát ebben az iskolában!
Jelöljük a fiúk (F) számát x-el, a lányokét (L) pedit y-al:
Év végén a fiúk p százaléka, azaz, 13 fiú lett kitűnő tanuló:
Év végén a lányok p+3 százaléka, azaz, 20 lány lett kitűnő tanuló:
A második megoldást a negatív eljőjel miatt elvetjük. Eszerint az egyetlen megoldás:
A 33 kitűnő (5,0 átlagú) tanuló közül sorsolással kiválasztanak hármat, akik ingyenes nyári táborozást nyernek.
b) Határozza meg annak a valószínűségét, hogy a kisorsolt tanulók között 1 fiú és 2 lány lesz!
Látnunk kell, hogy ez egy visszatevés nélküli mintavételezés!
13 fiúból kell egyet és 20 lányból kell kettőt választani. Ezek szerint a kedvező esetek száma eszerint:
Az 510 tanuló év végi tanulmányi átlagairól (a kitűnők számán kívül) még a következő információkat tudjuk: az év végi átlagok terjedelme 2,4; módusza 3,8; mediánja 4,0; átlaga 4,2; szórása 0,9; alsó kvartilise 3,3; felső kvartilise 4,6.
c) Készítsen a tanulók év végi tanulmányi átlagairól sodrófadiagramot!
A sodrófadiagramhoz öt adat szükséges:
Mivel van kitűnő tanuló az osztályban, ezért a maximális érték: